AIモデルの透明性についての基本概念と手法

AI・機械学習モデルの透明性は、AI・機械学習の誕生当初からのテーマですが、今日、ますます重要なテーマとなっています。その理由は、エンタープライズAIアプリケーションが普及し、ディープラーニングなど機械学習のブラックボックスモデルが飛躍的な進歩を遂げ、さらに多くの個人データがAIモデルで使用されていることに対して人々の懸念が高まっているためです。

さまざまな状況で使われる「AIの透明性」は、概ね次の点に集約されます。

• 解釈可能性・説明可能性
• 再現性・トレーサビリティ 
• 倫理性・信頼性・公平性

このブログでは、AIの透明性の最も基本的なレベルに焦点を当て、入力変数、つまり特徴量が予測精度の向上にどれだけ寄与しているかを説明する方法をご紹介します。評価手法は多数ありますが、代表的な手法とそれぞれのメリットとデメリットを以下にご説明します。

線形モデルの線形係数

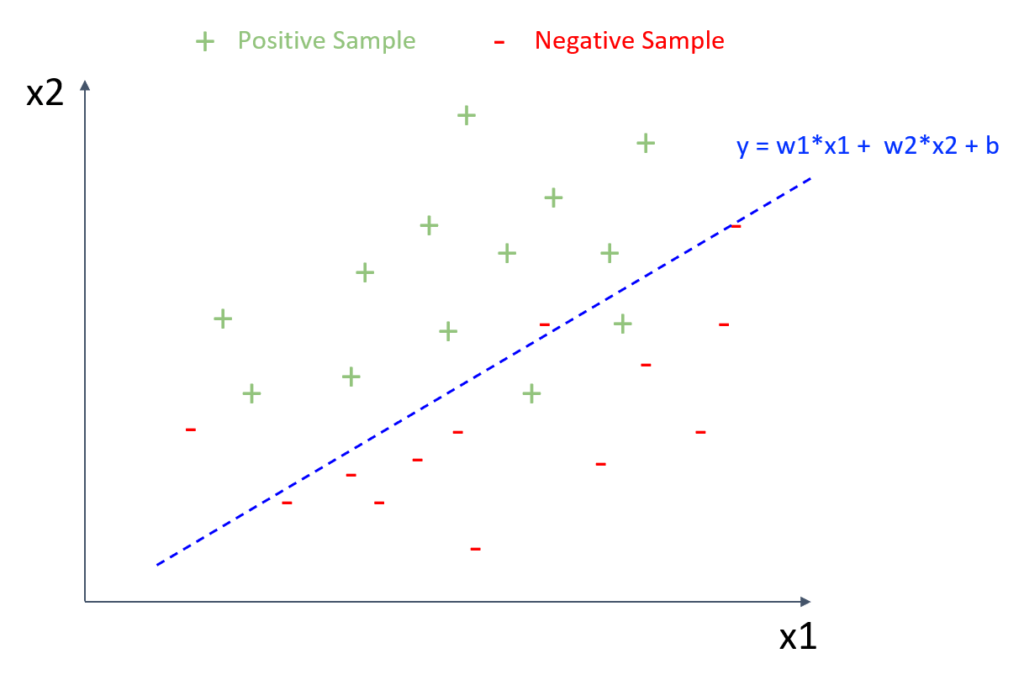
特徴量の線形係数 (重み) は、最も単純でありながら重要な手法です。図1は、単純な2次元の例 (「x1」と「x2」の2つの特徴量) に基づく線形係数の概念を示し、正のクラスと負のクラス（正例と負例）に属する複数のサンプルを表示しています。青い破線の直線が正のクラスと負のクラスを適切に区分してます。

この線形モデルは、「y = w1*x1 + w2*x2 + b」と表すことができます（中学の数学で習った1次関数を思い出してみましょう）。 例えば、x1に1を足すと、yは比例してw1増えます。x2とw2についても同様です。したがって、w1とw2の係数は、x1とx2の変数（特徴量）がこのモデルの予測の精度にどれだけ寄与しているかを表していると考えることができます。

線形係数の利点は、（1）単純で分かりやすい、（2）各特徴量の寄与度を正確に表わす、（3）係数はモデルのパラメータとして利用できるので、さらに計算を行う必要ない、などが挙げられます。一方で、この手法の最大の欠点は、主に適用できるのは線形モデルのみということです。

局所的な線形近似

図2は、図1と同じサンプルを使用した例ですが、「y=f(x1,x2)」という非線形モデルで表わしています。「f」 はブラックボックス関数を示します。このようなブラックボックスモデルを説明する一般的な手法の1つは、線形モデルで予測関数を局所的に近似させることです。例えば、予測境界線は、図2のP1付近でピンク色の線を引いた線形モデルや、P2付近でオレンジ色の線を引いた線形モデルで近似できます。

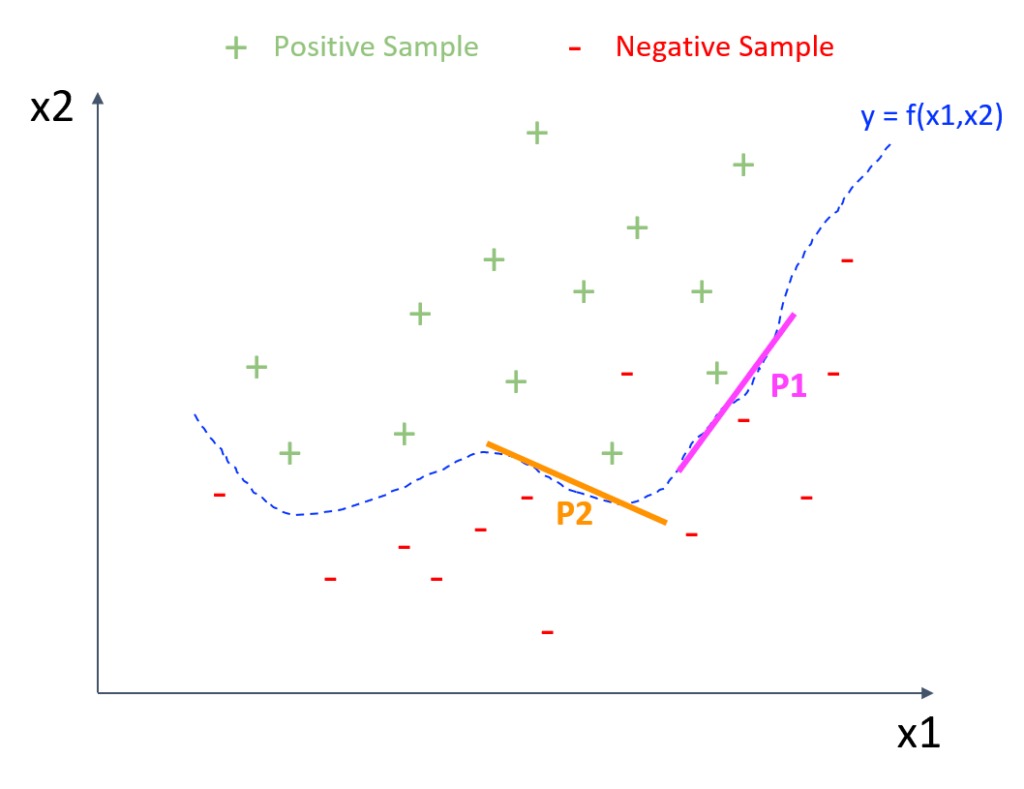
それぞれの「局所的な線形」モデルで、「線形係数」の説明を適用できます。局所的な解釈を可能にする手法にはさまざまなモデルがありますが、LIMEはその代表的なものの一つでしょう。このアプローチの利点は、基本的にはあらゆるブラックボックスモデルで説明が可能なことです。しかしながら、このアプローチに対する最大の批判の１つは、特徴量が高次元である場合、線形近似の信頼性が極端に低下するということです。特徴量が高次元になると、同じ精度を実現する予測境界線は無限に存在することが一般に知られています。実際、学習データに小さな摂動を加えると、LIMEは非常に異なる線形係数を返すことがよくあります。

Permutation Importance

「次元の呪い」を回避し、各特徴量の予測精度への影響度を確実に測定するための一般的な手法は、他の特徴量を考慮しつつ、特徴量を 1つ1つ評価することです。代表的な手法は、特徴量の値をランダムに並べ替えて特徴量の重要度を測るPermutation Importanceで、scikit-learnやeli5などの主要なライブラリで利用が可能です。

図3は、この手法の概念を示したものです。特徴量の重要度を計算するには、まず、重要度を測りたい特徴量をランダムに並べ替えた別のデータを作成し、この並べ替えた後のデータに対する精度を評価します（図3のAccuracy-2）。ターゲットの特徴量がランダムにシャッフルされているため、並べ替え後データの精度（Accuracy-2）は、元データの精度(Accuracy-1)よりも低いことがよくあります。乱数によるばらつきを抑えるために、ランダムな並べ替えを数回繰り返し、並べ替え後データの平均精度を計算します（Accuracy-2-ave）。そして、元データの精度(Accuracy-1)と並べ替え後データの精度（Accuracy-2-ave）の誤差を測定します。直感的に言えば、ランダムな並び替えは、特徴量とターゲット変数の依存性をターゲットの特徴量の相関を排除し、それによる精度の変化から、その特徴量の重要度を測るというアイデアです。

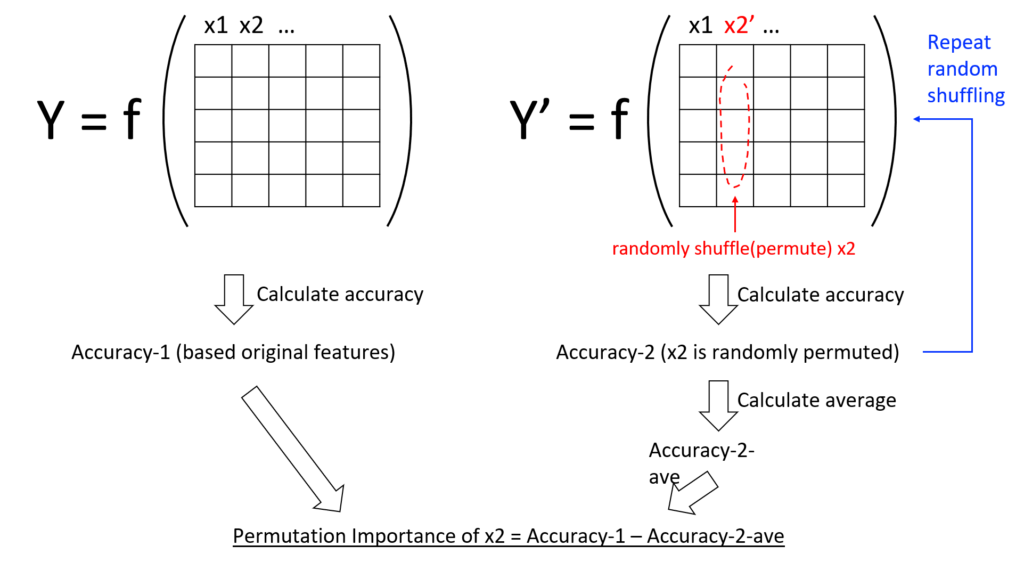
この手法では各特徴量が1つずつ評価されるため、特徴量が高い次元に対して、より信頼性の高い手法となります。また、この手順は、あらゆるブラックボックスモデルで適用でき、精度やエラーの指標を算出できます。

このブログでは、AI モデルの透明性に関する基本的な概念と手法を説明しましたが、 他にも、Sharply Valueを近似的に算出するSHAP、Impurity-based feature importance、頻度ベースの特徴量重要度（frequency-based feature importance、勾配ブースティング向け）など、多くの手法があります。

まとめ

モデルの透明性とは、最終的な予測に対する特徴量の影響について説明が可能であることを意味します。特徴量を評価する一般的な手法としては、特徴量の線形係数、局所的な線形近似、Permutation Importanceなどがあります。線形係数は分かりやすく、計算の必要もありませんが、線形モデルにしか適用できません。2つ目の局所的な線形近似では、理論上はあらゆるブラックボックスモデルも説明可能ですが、特徴量が高次元になると線形近似の信頼性は非常に低くなります。3つ目のPermutation Importanceは、高次元の特徴量を扱うことができ、また主要なライブラリで利用可能なため、比較的使いやすい手法です。

後半のPart 2「不均衡（アンバランス）・高次元データに対するブラックモデルの透明性向上」では、Permutation Importanceについて、具体例を挙げてさらに詳しくご説明します。