時系列データの特徴量設計 – パート2

このシリーズの「時系列・時間データに関する特徴量設計 – パート１」ではARモデル、ARIMAモデル、LTSM､Prophetといった標準的な時系列モデルに焦点を当てました。時系列モデリング手法は現在でも広く使われていますが、異なるデータ特性や時間分解能を扱うことができない、時間的トランザクションをサポートしていない、モデルの説明可能性や透明性が低いといった問題があります。

2回目となる今回は、時系列データを扱うための代替アプローチとして、時間データセットからの特徴量設計について、その利点と共に解説します。具体的には、3つの異なるタイプの時間的データ、それぞれに対する特徴量の設計方法と特徴量の例、そして特徴量エンジニアリングがどのように標準的な時系列モデリング手法の問題点を解決するのかについて見ていきます。

時系列データとは（時間的データの種類）

時間的データとは、各レコードに対してタイムスタンプが付いているデータです。

時系列データとは、毎日の株価、毎週の売上高、毎月の在庫水準など、一定の時間間隔を持つ値で構成されます。需要予測、販売予測、価格予測などの時系列予測のために、企業向けAIアプリケーションにおいて、最も一般的かつ不可欠なデータタイプの1つです。

トランザクションデータ（または時間的トランザクションデータ）は任意のタイムスタンプを持つトランザクションレコードで構成される、もう1つの代表的な時間データであり、たとえばPOS（販売時点情報管理）の取引記録、ウェブログ、障害警告のログトランザクションなどが挙げられます。

イベント/カレンダーデータは給与の支払日、休日、キャンペーンスケジュールなど、特定のタイムスタンプに紐づいたイベントをまとめた時間的情報です。下に示す図1でこれら3つのタイプの時間的情報をまとめています。

本シリーズのパート1で説明した時系列モデリング手法は、時系列データのみに適用可能ですが、他の２つの時間的データも重要な情報源です。

特徴量設計に基づく時系列モデリング

特徴量設計は、従来の時系列モデリングに代わるアプローチとして非常に有用です。特徴量設計に基づく時系列モデリングでは、まず、時系列データを特徴量の一枚表に変換します。次に、何らかの機械学習アルゴリズムを特徴量テーブルに適用し、予測モデルを学習します。従来の時系列モデリング手法が時系列の振る舞いをモデル内に取り込むのに対し、この代替アプローチは時間情報を特徴量としてモデル化していると言えます。

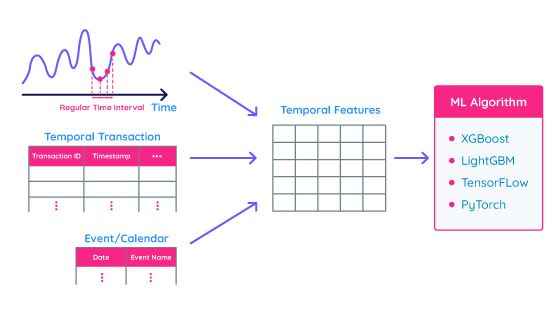
特徴量設計を使ったアプローチは、従来の時系列モデリング手法のさまざまな欠点を克服し、高度な時系列/時間予測モデルを開発するためのシンプルかつ柔軟な方法です。たとえば、異なる時間解像度のデータを扱うために異なる時間解像度を持つ特徴量集約関数を適用したり、異なるデータ特性を持つ時系列に異なる特徴量エンコーディング手法を適用したりといった具合です（たとえば、数値時系列に対する単純平均エンコーディングや、カテゴリ系列に対するカテゴリカウントエンコーディング）。特徴量設計のアプローチは、トランザクションとイベント/カレンダー情報を単一の特徴量テーブルとして自然に統合することも可能です。さらに、特徴量の複雑さと最終的なモデルの精度のバランスを考慮することで、モデルの透明性と解釈可能性を両立することができます。

時系列データに対する特徴量の例

ラグ特徴量（ラグ値の集約）

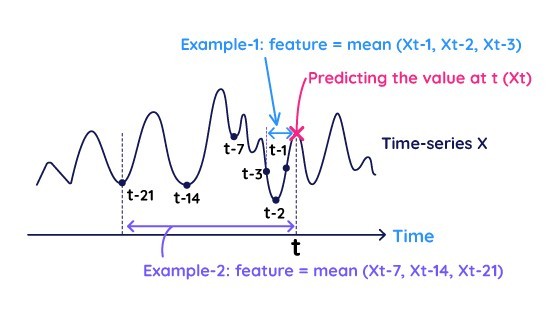
時間集約は、時系列データやトランザクションデータから特徴量を抽出するための基本的かつ柔軟性の高い方法です。時間集約特徴量は2つの項目で定義されます：1) 集約するデータの範囲（ラグ）、2) 選択した範囲内の複数の値を集約する方法

図2は時間集約特徴量の例を示しています。Example-1は直近のレコードを集約することで特徴量を生成する例です（本シリーズのパート1で説明した自己回帰モデルとほぼ同じ効果を持ちます）。Example-2は7日周期によってレコードを集約し、週次のパターンを捉える特徴量を生成しています。これらの例では集約関数として「平均」を用いていますが、異なる集約方法（最大、最小、標準偏差など）によりほかの時間的挙動（つまり異なる特徴量）を抽出可能です。

時間間隔特徴量

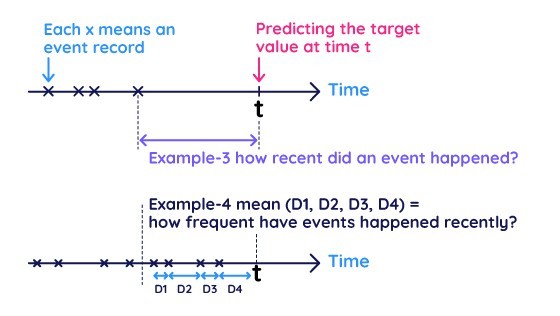
「時間間隔」は、トランザクションデータから特徴量を導き出す強力な方法です。図3で時間間隔による特徴量の2つの例を示しています。Example-3はあるイベントがどれだけ最近発生したか（最新のレコードまでの時間間隔）を特徴量化しており、Example-4はあるイベントがどれだけ頻繁に起きたか（一定期間の時間間隔の平均値）を測定したものです。これらの時間間隔特徴量はコンシューマ・マーケティングや行動分析におけるRFM（Recency、Frequency、Monetary）モデルと高い関連性を持っています。時間間隔特徴量は2つの特定のタイムスタンプを元に抽出可能です。たとえばニューヨークのタクシーデータセット（Kaggleのコンペで非常に有名なデータ）では「乗車時間」と「下車時間」の間隔が、運賃と相関の高い乗車時間を表現しています。

タイムスタンプと時間的イベントの特徴量化

タイムスタンプそのものを特徴量にすることもできます。たとえば「2022/3/15 09:00:00」を「3月」や「朝」といったカテゴリ値に変換すればカテゴリ変数に対するエンコーディング手法を適用可能です。このようなタイムスタンプの特徴量化は生のタイムスタンプから文脈情報を抽出でき、モデル性能の向上に役立ちます。もう1つの一般的なアプローチは、イベント/カレンダー情報から二値フラグ特徴量を作成するものです。たとえば休日カレンダーに基づいてタイムスタンプを休日フラグ特徴量に変換できます。このような休日フラグ特徴量により、休日の商品需要（たとえばブラックフライデーの小売商品販売）の精度が大幅に向上することはよく知られています。

そのほかの時間的特徴量

時間的特徴量を抽出する方法はほかにもあります。指数荷重移動平均（EWMA）は時系列ボラティリティ分析に広く用いられ、より長期の移動平均の効果を捉えることが可能です。フーリエ変換は製造業のセンサーデータでよく使われ、時系列の特徴を周波数領域で捉えます。連続ウェーブレット変換は周波数と時間の両領域で特徴量を抽出します。利用可能な時間的特徴量の数と種類は増え続けており、特徴量設計アプローチはそれらを活用可能です（tsfreshなどのOSSはさまざまな時間的特徴量をライブラリとして提供しています）。

まとめと次回予告

現代の時系列分析や時系列予測では、特徴量設計に基づくモデル作成のアプローチが、広く利用されるようになっています。時系列予測に対する特徴量設計アプローチの利点は、任意の特徴量を設計することにより、より多くの情報をモデルに取り込めるという柔軟性です。また、抽出した特徴量を高度な機械学習手法に適用することで、予測精度を最適化することができます。

次回のパート3では、代表的な時系列モデリングであるARIMAモデル、Prophetと特徴量に基づくアプローチの比較について解説します。

dotDataが企業における時系列予測にどのように活用できるのか興味がある方は、ぜひお気軽にお問い合わせください。