時系列・時間データに関する特徴量設計 – パート１（時系列モデル概説）

時系列分析と時系列データ

時系列データとは（或いは、タイムスタンプ付きデータとは）、需要予測、販売予測、価格予測など、企業向けAIアプリケーションにおいて、最も一般的かつ不可欠なデータタイプの1つです。時系列データを分析すること（時系列分析）で、時間の経過に伴う潜在的なパターンを見つけ出し、将来の予測を実現します（時系列予測）。一方、優れた時系列モデルを開発することは、企業のデータサイエンス及び分析チームにとって、重要でありながら非常に難しい課題です。

このブログシリーズでは、時系列データとタイムスタンプ付きデータからAIやMLモデルを開発するためのさまざまな時系列予測のアプローチについて概観します。3回にわたってお届けするこのシリーズの初回として、今回は一般的な時系列予測と時系列分析手法についておさらいし、その特徴、利点、及び制約について解説します。

標準的な時系列モデリング手法

自己回帰モデル

自己回帰モデル（ARモデル）とは、最も直感的で伝統的な時系列モデリングのための統計手法の1つです。このモデルは対象となる時系列上の過去から現在の値を入力として、将来の値を線形回帰によって予測することから「自己回帰」と名付けられています。ARモデルは時系列中の直近の値を入力として利用し、次の値を予測します。このモデルは、最近の時系列の挙動に基づいて次の挙動を説明（予測）できるという仮定に基づいたものです。ARモデルは単純であり、時系列モデリング技術の基本的な概念を理解するのに適しています。しかしながら、ARモデルは複雑な時系列の振る舞いを捉えるには単純すぎるため、予測結果が悪いことが多く、現代の時系列予測プロジェクトではほとんど使用されていません。

自己回帰和分移動平均モデル（ARIMAモデル）

自己回帰和分移動平均モデル（ARIMAモデル）は、ARモデル同様、過去の値に基づいて未来の値を予測するものです。ARモデルの弱点を克服するために、時系列データをなめらかにするために、「自己回帰和分移動平均」という名の通り、自己回帰、和分、移動平均という三つの要素に時系列データの挙動を分解し（これら三つの挙動は、時系列データに対する三つの異なる特徴量に相当します）、移動平均のような時間の経過に対して滑らかな変化をモデルに組み込むことができます。ARIMAモデルは天候のパターンや来月の売上高変動の予測など、さまざまな用途で利用価値があるモデルです。ARIMAモデルの欠点としては、非線形の依存性を持つケースにうまくできない、誤差が独立同時正規分布である必要がある、外生変数を利用できないことが挙げられます。ARモデルやARIMAモデルは、より一般的な状態空間モデルとして表現することも可能です。一方で、１）状態空間モデルは問題ごとのモデリングが必要になる、２）状態空間モデルを利用できるOSSが少ない、などの理由から、実際のプロジェクトではARIMAモデルが利用される傾向にあります。

長・短期記憶モデル（LSTMモデル）

長・短期記憶（LSTMモデル）とは、系列予測問題を解くための再帰型ニューラルネットワークです。LSTMには「メモリーセル」と呼ばれるより長期間にわたって情報を記憶することができる仕組みが含まれています。また、入力、出力、忘却の3つのゲートを持ち、どの程度のデータ（もし存在すれば）が次の層に渡されるか管理します。LSTMはより長期的な依存関係を学習しますが、同時にデータの短期的な順次動作をも捉えることが可能です。LSTMは従来の時系列モデルよりも高い予測精度を達成することが多いですが、すべての重要な要因（特徴量）が複雑かつ非線形な隠れ層に暗黙的に符号化されるため、透明性と解釈可能性に欠けるところが重大な欠点の1つです。LSTMはPyTorchやTensorFlowなどの一般的なディープラーニングフレームワークでOSSとして利用できます。

Prophetモデル

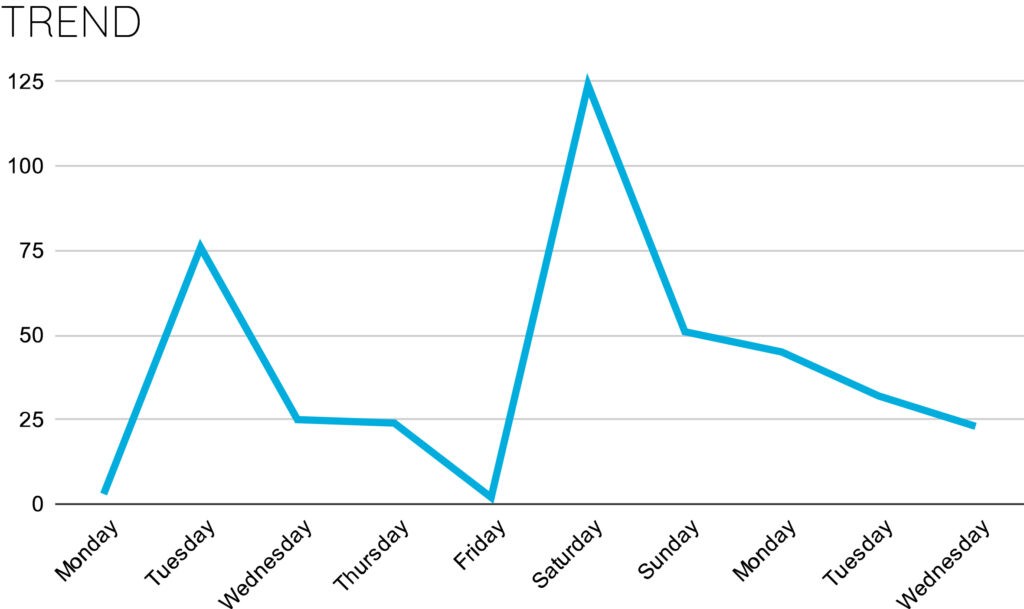
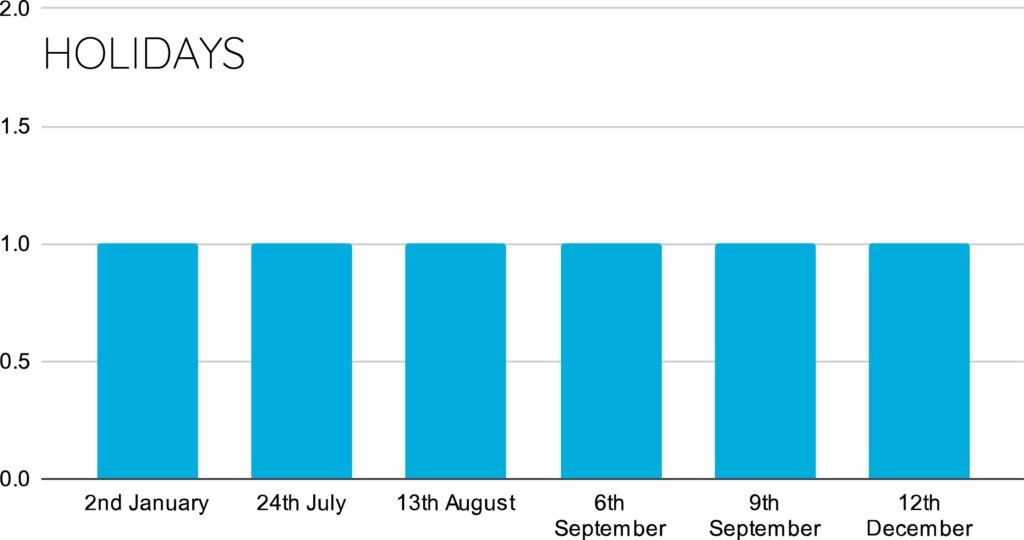
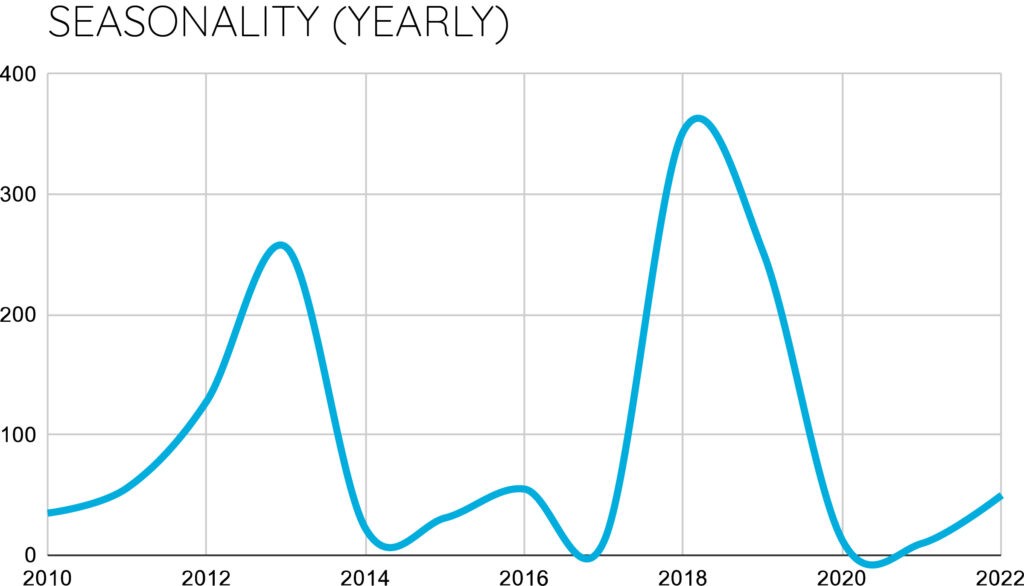
ProphetはFacebookが公開しているオープンソースのライブラリです。Prophetは非線形トレンドを考慮し、季節性（日、週、月、年）や休日の影響に適応できる加法モデルであり、特に強い季節性のあるデータに適した、実世界において強力で実用的なモデルといえます。Prophetを使う大きな利点は予測を作成するために深い予備知識を必要とせず、わかりやすく使いやすいパラメータを提供しているところです。

一方、ARIMAなどの他のモデルに比べて著しく性能が劣るという研究結果もあります。過去と未来のデータの因果関係を探すのではなく、Prophetモデルは線形ロジスティック曲線を用いてデータにフィットする最適な曲線を探しているためです。

時系列モデリングの限界

均質な時間分解能

通常の時系列モデルでは、一定の間隔で時系列データを収集する必要があります。また、多次元時系列を扱う場合、すべての時系列が同一の時間解像度を持つ必要があります（例：1時間単位、1日単位、1カ月単位）。これらの仮定や前提条件は現実の時系列データでは必ずしも成立しません（たとえばセンサーのサンプリングレートが一定でないなど）。このようなケースに時系列モデリング手法を適用するには、時系列データの前処理に工夫と時間をかけることが必要です。

均質なデータ特性

一般的な時系列モデリング手法は、暗黙のうちにデータの均質な特性を仮定しています。たとえば、数値とカテゴリの並びが混在する多次元時系列は扱えないことが多いです。実際の例として、時間帯ごとに店舗に入った人の数のような数値情報を収集するセンサーと、時間帯ごとに店舗でエアコンがオンかオフかという2値データを収集するセンサーがあるとします。これらの異質な情報を扱える時系列モデルとして状態空間モデルなど、より柔軟なモデルを利用することは可能です。しかし、ARIMAモデルで解説したように、個々のケースごとにコストをかけてカスタマイズしたモデルやアルゴリズムの開発が必要となります。

時間的トランザクションとイベント

時系列データは時間に関するデータの一例であり、時系列モデリング手法は時系列データのモデリングに特化したものです。しかしながら、ビジネスで蓄積されるデータには、時間的トランザクション（タイムスタンプ付きのトランザクション）や、イベント情報など時系列とは異なるタイプの時間データが存在し、それらを利用することで、モデルをより正確で高度なものにすることができます。

まとめ

このブログでは時系列予測モデルを構築するための標準的な時系列モデリング手法をまとめ、その特徴と限界について解説しました。連載の2回目では別のアプローチ、つまり時間的データに対する特徴量エンジニアリングについて見ていきます。

dotDataが企業における時系列予測にどのように活用できるのか興味がある方は、お問い合わせください。