不均衡（アンバランス）・高次元データに対するブラックモデルの透明性向上
- ブログ
dotData
dotData
このブログの前半のPart 1 「AIモデルの可視化についての基本概念と技法」では、線形係数、局所的な線形近似、およびPermutation Importanceなどの一般的な手法についてご説明しました。特に、特徴量の値を並べ替えて特徴量の重要度を測るPermutation Importanceは、あらゆるブラックボックスモデルおよび精度関数や誤差関数にも適用でき、すべての特徴量が同時に処理されるのではなく各特徴量が1つ1つ処理されるので、高次元の特徴量に対して信頼性の高い手法です。
ところが、Permutation Importanceは、計算コストが高いという欠点があります。特徴量の数、特徴量の値をランダムに並べ替える回数、モデルの数などの要素を計算に入れて評価を繰り返す必要があります。計算時間を短縮させる一般的なアプローチとして、回帰の場合や判別で正例と負例のバランスが取れている場合には、ダウンサンプリングを適用することもできます。一方で、単純なダウンサンプリングは、Permutation Importanceの信頼性を著しく低下させる可能性があります。
不均衡データでPermutation Importanceを使用
データサイエンティストのグローバルコミュニティであるKaggleのクレジットカード不正検出データセットを使用して、単純なダウンサンプリングを行うことで、Permutation Importanceの結果が不安定になってしまうことを検証してみます。このデータセットは、Kaggleコミュニティの間でよく利用され、不均衡データを使用した判別モデルのユースケースの典型例として知られています。データに含まれるのは、2日間に発生した284,807件のクレジットカード取引で、うち不正取引が492件（0.17%の正例）、特徴量が、V1～V28、時間、取引金額の合計30次元です。目的は、このデータを用いて不正取引を検出するモデルを構築することです。この実験は次の条件で行いました。
- Intel Core i7-9750H（6コア）のCPUを搭載した標準的なノートパソコン
- eli5とXGBoostのライブラリ
- AUC（ROC曲線の下側の面積）を精度の指標として使用
- シャッフルの回数は5回（eli5のデフォルト値）
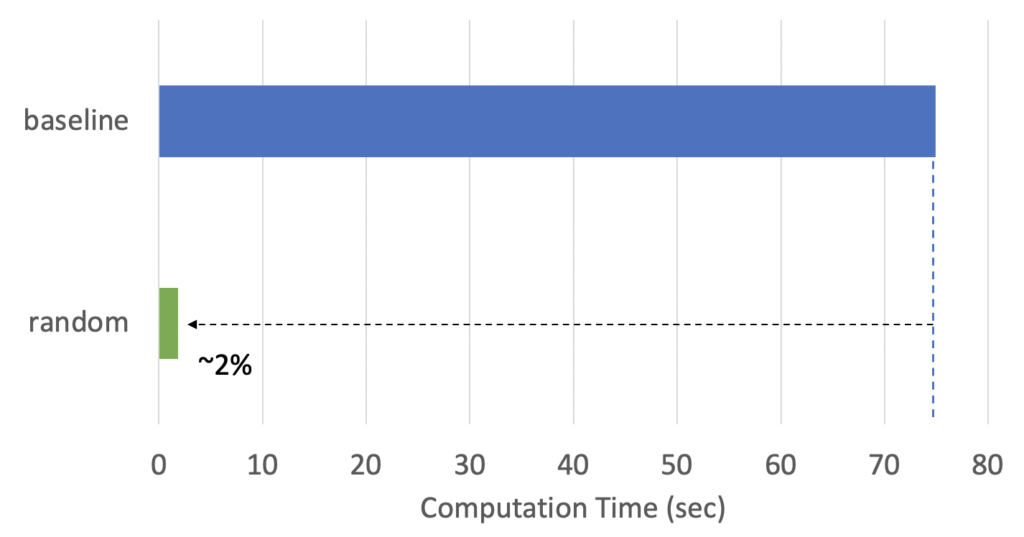
図4は、Permutation Importanceの計算時間を示しています。図4の「baseline（ベースライン）」では、eli5を使用し、全データを利用しています（ダウンサンプリングなし）。計算にかかった時間は約75秒です。75秒は短時間と感じるかもしれませんが、仮にデータセットに含まれる特徴量が30次元の代わりに、300次元あり、10モデルを比較するとしましょう。すると、計算時間は7,500秒、つまり2時間以上かかることになります。計算時間を短縮する合理的な方法の１つは、ダウンサンプリングを行うことです。図4の「random（ランダム）」は、5,000件のサンプル（元の母集団の約1.7%）を無作為に抽出するランダムサンプリングを適用しています。ご覧のように、計算時間は比例して減少しています。
次に、図5は、Permutation Importanceの計算結果を「baseline」（青）と「random」（緑）で示しています。「random」手法で計算したPermutation Importanceは、「baseline」手法での計算結果とは大きく異なります。さらに、推定値の分散（5回のランダムシャッフル全体の標準偏差）が非常に大きく、「random」手法による計算結果は信頼性に欠けることがわかります。
高速で安定したPermutation Importance
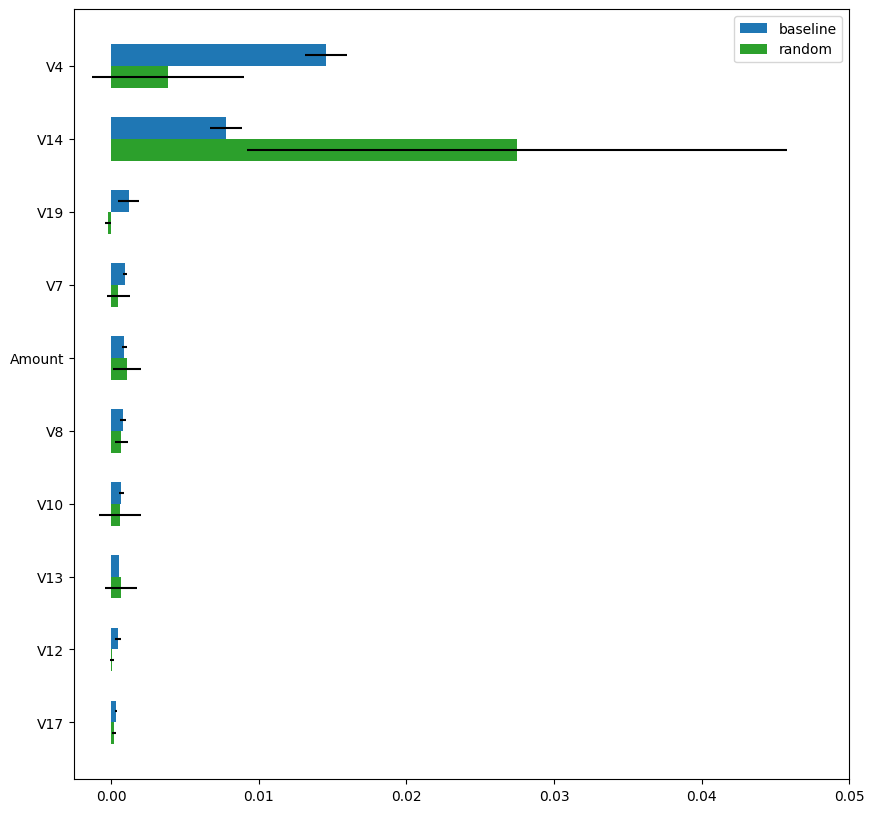
不安定な計算結果になる主な理由は、単純なダウンサンプリングをすると、元々少数の正例の数がさらに減少するためです。上記の例では、ダウンサンプリング後、正例は平均して8～9件（492件の正例の1.7%）しか含まれていません。したがって、各ランダムシャッフル後のデータに含まれる8～9件のみの正例に基づいて評価されるため、Permutation Importanceの計算結果は当然不安定になります。より多くの正例を含めるために、層化抽出法（正例と負例がバランスするようにサンプリングする）を検討することもできますが、この手法では、正クラスと負クラスの分布が変化してしまいます。つまり、層化抽出法を適用した前後で、正例と負例の比率が変化してしまうため、正しく特徴量の重要度を評価することができません。
dotDataでは、独自の高速かつ安定したアルゴリズムを使用して、クラス比率が不均衡なデータのPermutation Importanceを算出します。このブログでは、アルゴリズムの技術的な詳細には触れませんが、概念は次のとおりです。
- 母集団全体のサイズを小さくする一方で、層化抽出法を適用して、より多くの正例を抽出する。
- 層化抽出法による分布の変化の逆変換を適用することによって、特徴量の重要度の評価を補正する。
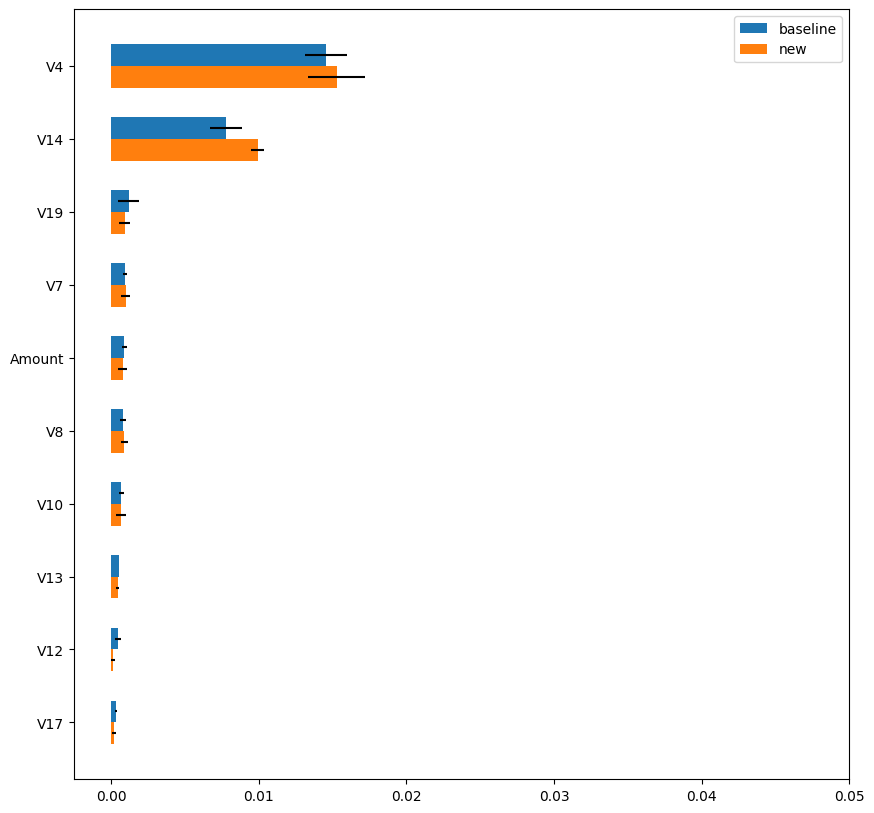
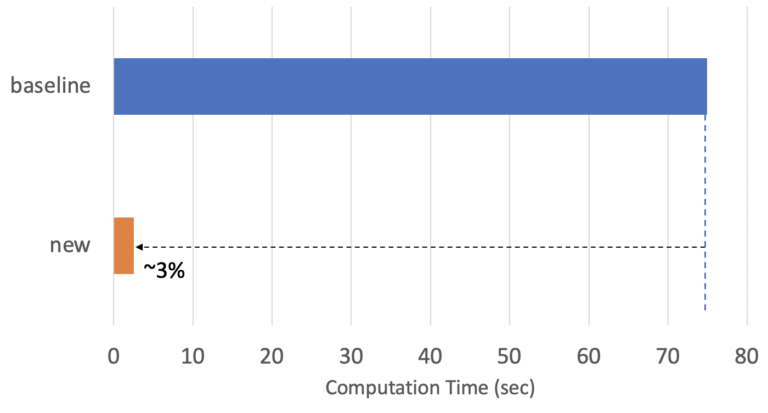
図6は、「baseline」手法とdotDataの「new」手法で算出したPermutation Importanceの結果です。「new」手法は「baseline」手法とほぼ同様の評価結果を示し、推定値の分散は図5の「random」手法と比較すると、はるかに小さいことがわかります。図7は「new」手法の計算時間を示しています。「new」手法の計算時間は「baseline」手法のわずか3%であり、安定した信頼性の高い評価を行いつつ、30倍以上の高速化を達成しています。
キーポイント
2回にわたるブログ記事では、不均衡データに対するブラックボックスモデルの透明性に関する手法について説明しました。重要なポイントは次のとおりです。
- AI・機械学習モデルの透明性は、企業におけるAI・機械学習モデルの最も基本的で重要な側面の1つとなっています。その理由として、モデルの利用者とって解釈が可能であることや、特に金融業界などの規制の厳しい業界で説明責任が求められていることなどが挙げられます。
- 業務で判別問題を行う場合では、判別クラスが非常に不均衡なことがよくあります。一般的なモデル透明性の手法を不均衡なデータに適用しても、ほとんどの場合、推定値の信頼性が非常に低くなるか、計算量が多すぎて実用的ではありません。
- dotDataは、安定性と計算時間の両方を大幅に改善する独自のアルゴリズムを開発し、不均衡なデータや高次元データに対するモデルの可視化を向上させました（このアルゴリズムはdotData Enterprise 1.6 および dotData Feature Factory 1.2以降に実装されています）。
dotData
